に移動してもAB”の距離がD’と同じになれば波がAから四方に出ているときは同じことがいえる。

さて、Bがf秒かかってB’にきた。t秒間にAからBに到着する波の山数はf×tであることは前述のとおりであるが、BがB'にくるとAB’の間にはD’/λしか波が入っていないからBがBに来るt秒間だけ受信点は余分に波を受けなければ勘定が合わない。したがってBからB’に移動する受信点がt秒間に受取る波の振動数N：は、

である。受信点の移動雄をν（m/sec）とすると、t秒間に動く距離はνtでνt＝（D−D’）であり、前述のように

である、c＝1秒のときは、

となり、前述のf'＝f（c＋ν）/cが導かれたことになる。

こうして、送信の周波数と受信した周波数あるいは受信波の山の数が明らかになれば、受信点の移動距藤や移動速度（送信点が固定のとき）、正しくは送受信点間の視線速度が求まることになる。

このような、周波数の計測は鉛の無線室などにもある周波数カウンタあるいは万能カウンタという測定器で容易に測定できる。周波数カウンタでは測定器の中に時計があって、1秒間に受けた波の山数を数えて、数字表示菅で示しているので、それがただちに周波数であるとすることができる、また万能カウンタでは外から別に時間の信号を入れることもできるので、B点の動いた任意の一時間だけ波の数をかぞえ、送信の波長λと送信周波数からその時間に動いた距離を求めることもできる。

ドプラ効果の原理を使って、人工衛星を利用して船の位置を求める方法が可能かどうかについてまず考えてみよう。いま、簡単化のために、衛星の軌道を図3.6のように直線と考える。そして、その衛星がν、たとえば秒速8?というような速さで、その直線上を進む、図のような受信点で、その電波を受信していると、受信点と衛星との間の距離は時間tとともに変化するので、その距離Dは、tの関数ということでD（t）という形で表わされる。衛星の刻々の位置Sも当然tの関数となる。このとき衛星から安定な周波数の電波を送信していると、受信点での受信局波数はドプラ効果により下の図のように変化する。この図の縦軸はドプラ周波数、すなわちドプラシフトの値4fを示す。4fもまた時間の関数である。

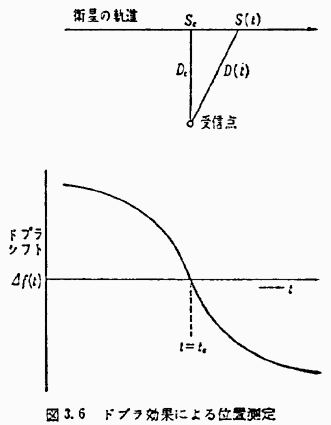
衛星が最も受信点に近づいた点をSeとする。このときの時間はtcで、また、そのときの衛星の受信点の距離をDeとする。前にも述べたように、このときには衛星と受信点との距離がだんだん近づいてきて、この点以降は逆に遠ざかるのであるから一瞬間、衛星と受信点との間の速度は0になり、受信周波数は送信周波数に等しく、4f＝0となる。

この時間が何かの方法、たとえば送信周波数がわかっているとか、あるいは上図の曲線（ドプラ曲線）の曲率が逆転する瞬間をとらえるかなど、によって測定できたとすれば、受信点はSeを通り衛星軌道）に直交する平面（この平面と地球面の交わりは1本の位置の線になる）内にあることになる。図3・6で直角三角形の定理から、

D（t）＝｛Dc2＋ν2（t−te）2｝1/2 （3.5）

ここでνは前に述べたように衛星の軌道がわかれば衛星の速度v（必ずしも

前ページ　　　目次へ　　　次ページ